home -> projects -> Initial experiments with training Multi-Layer Sparse Autoencoders

Initial experiments with training Multi-Layer Sparse Autoencoders

TLDR: I train many different sparse auto-encoders on a mixture of MLP output activations, trying different methods to improve their performance. The more invasive methods don’t do much, but some models are still able to learn features which generalize across layers in interesting ways. These models were also hindered by a low expansion factor chosen due to the need for large hyperparam-sweeps, further tests with a larger expansion factor have performed better.

I’m curious about whether or not features learned by sparse autoencoders can be generalized across multiple layers of a model. More specifically, are there features in the write-outs to the residual stream from different layers that occur within the same latent space? To test this, I train a sparse autoencoder on a mix of activations from multiple layers, and use it to attempt to detect interpretable features across different layers. There are a few reasons why I find this interesting:

  1. If a sparse autoencoder could be trained on the outputs of many layers at once, perhaps the features that it learns would be more generalized
  2. It could also be a interesting tool for understanding the relations of layers on the level of features,
  3. If some subset of all of the features is common to many layers within a model, would it be possible to take an autoencoder trained on those features, and then further train it on individual layers? If so this could speed up training in a way that scales well with layer count.

From the start I see some immediate challenges with this:

  1. The norm of each layer’s output to the residual stream grows with further layers, which may lead to later features having a higher reconstruction loss and thus being over prioritized during training. This may be addressable by scaling activations depending on their layer of origin, but it may be more complicated, see here1
  2. Two features from different layers may fully co-occur and point to the same general feature, but if they are represented differently in any number of ways, naively treating them as interchangeable seems unlikely to result in a single feature being learned during training. In general, I am broadly uncertain about the self-consistency of the residual stream, since there doesn’t seem to be particularly strong pressure for its space to remain the same across the length of the model.

For all of the following tests I use GPT-2 small and TinyStories.

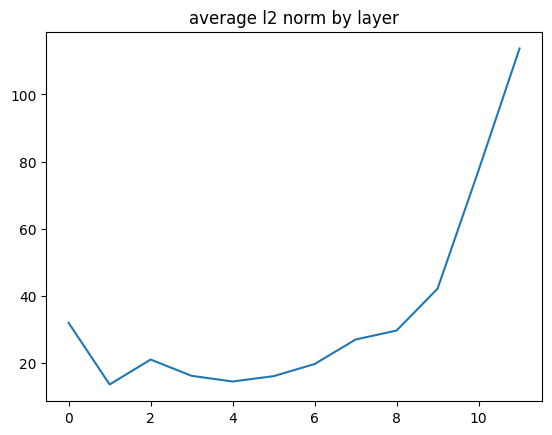
Before training the model, I wanted to attempt to address the potential issue mentioned above of the average norm from the output of the MLP layer changing across the layers. I ran a test calculating this for the model and dataset I was using, shown below.

img

The issue that I suspected this would cause is that later features are over prioritized during training. The post linked above hypothesizes that the growing norm is an artifact which arises out of the difficulty of erasing anything from the residual stream, which makes overpowering it a more likely strategy for the model to learn. It still seems plausible to me that this effect doesn’t account for the entirety of the trend, and that perhaps different layers do output different amounts of information/features, and the naive method of accounting for this trend could cause more issues. This is all very speculative, and so I run some tests later on to test some different approaches.

Before getting to those tests, I first had to find a good configuration for training the different layers, and test how they performed individually. I began with running a sweep across 8 different lambda regularization factors for each of the 12 layers. The full results can be seen here2, but the most relevant piece is shown below - the FVU vs L0, for each layer. (For the interactive version, see the link)

img

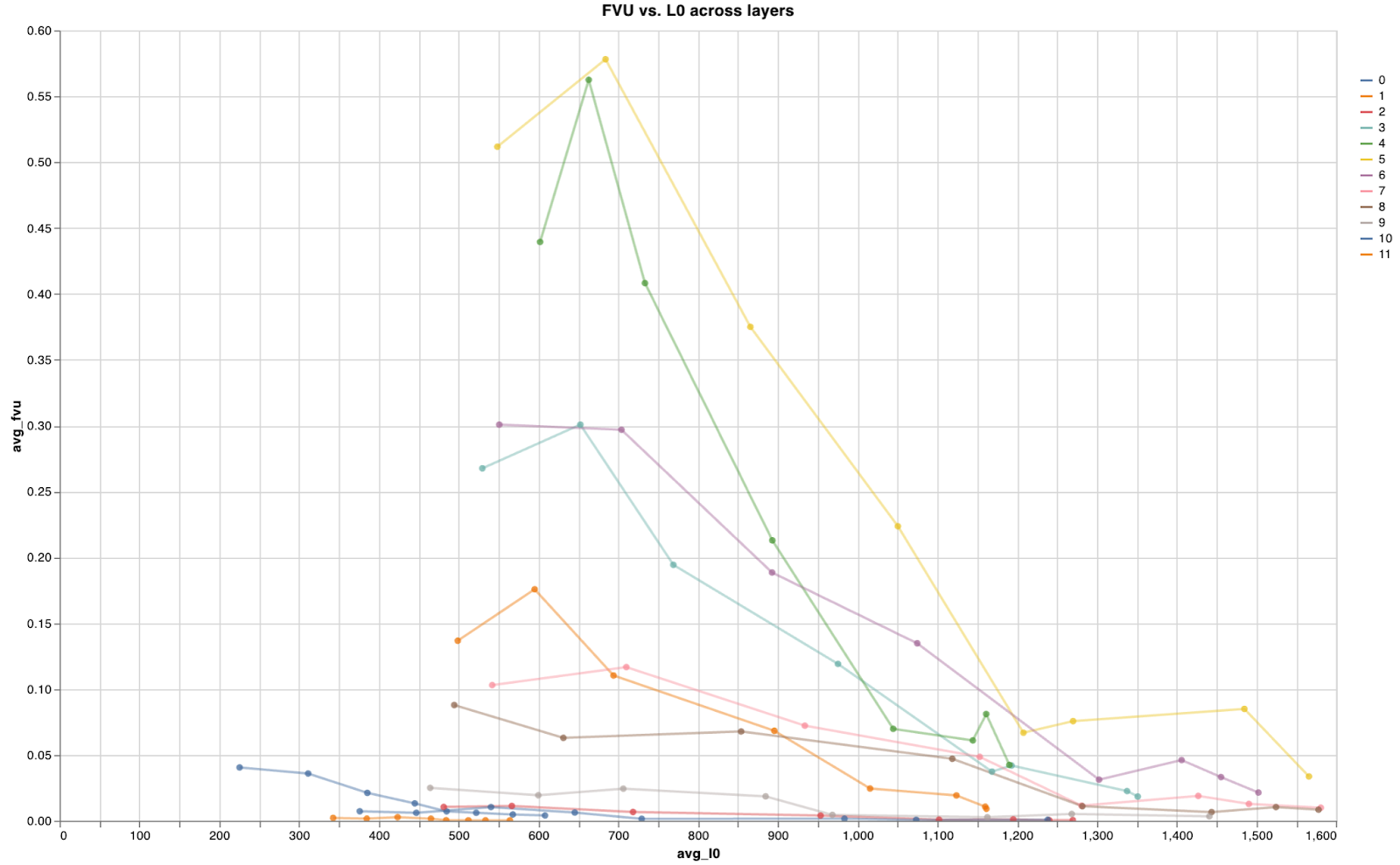
The pareto front between fvu and sparsity seems to follow a similar concave trend to the norm of the feature activation, with the early and final layers being shifted down/left, and the middle layers up/right. We even see the same pattern of layer #1 being a local outlier to this curve. This makes sense, if the set of activations for each layer is approximately centered, since in that case the average of the variance of each feature should be approximately equal to the average of the squared l2 norms.

I don’t think that this explains the entirety of the shift however, since the average l2 norm is higher on the later layers compared to the earlier layers, but the down/left shift of the fvu-sparsity front is more even between early and later layers.

The exact implications this has for training a multi-layer autoencoder are unclear - it does push me further towards believing that there is a gradient of something like # of “true” interpretable features across layers that is not shown through the average norm per layer. The clusters here may also suggest some layers which would be good to train together, e.g. 3, 4, 5, and 6, since they seem to have similar characteristics. This is all highly speculative, but worth testing.

It also makes me curious about the effect of using a different L0 regularization factor for different layers within the same multi-layer autoencoder. My intuition is that this makes no sense, but I’m curious nonetheless.

Next, I ran a sweep training an autoencoder on a mix of all layer’s activations, using 4 different activation rescaling functions, at 3 different learning rates and 4 different lambda regularization factors. The four rescaling functions tested were linear, square root, log, and not rescaling anything. These functions are applied to the average L2 norm per layer calculated above, and the result is used to calculate scaling factors for each layer which normalize them to the mean. The primary results can be seen here3, and all data collected can be seen here4.

The results show that using this technique increases both the average L1 and MSE, averaged over all layers, over the length of the run - not good.

However, broken down into average L1 and MSE by layer (shown below), we see a more interesting effect.

img

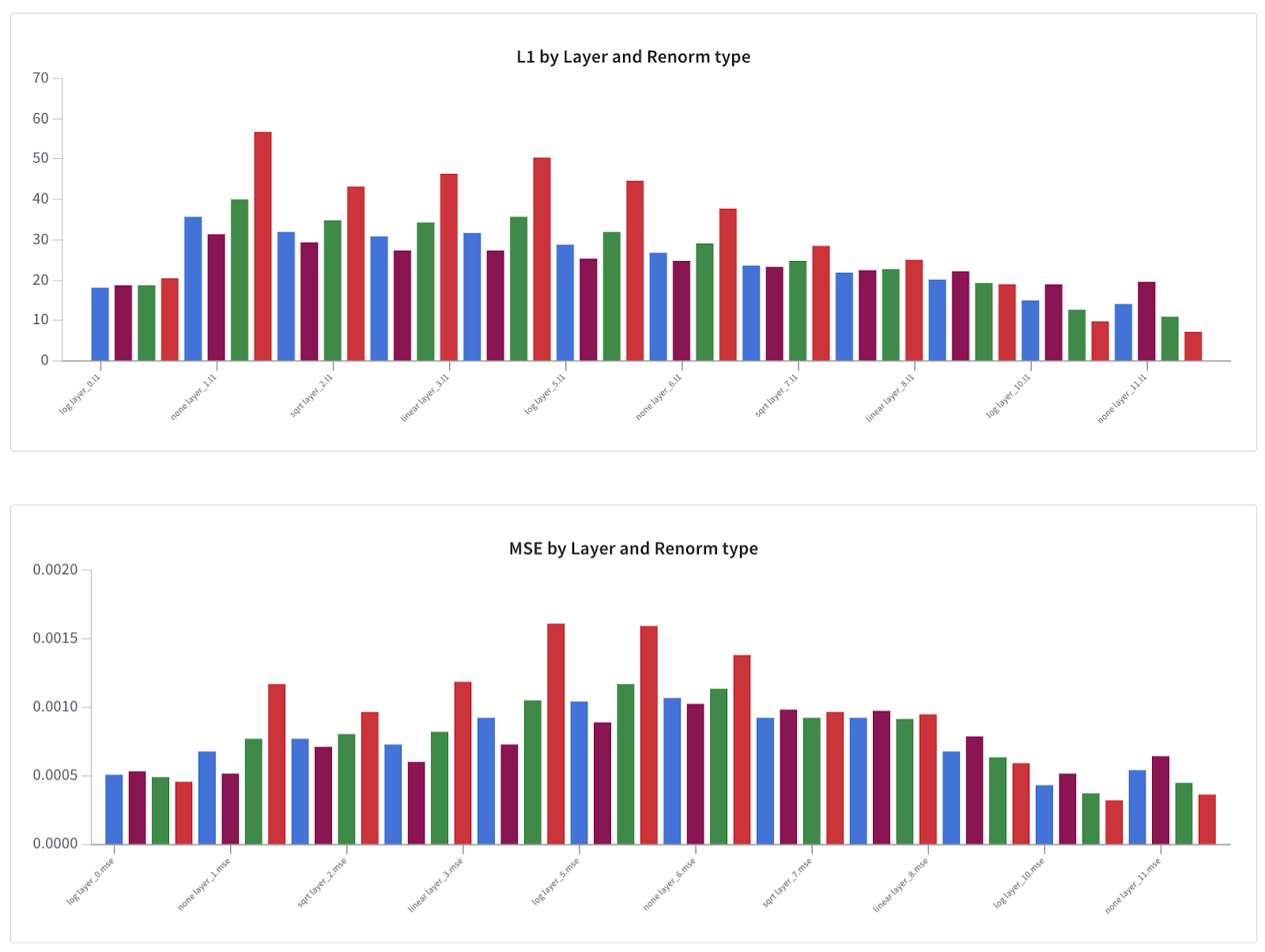
(The color of the bars represents the rescaling type used. See the interactive version in the link above, or just know that blue is log, purple is none, green is sqrt, and red is linear)

L1 follows the trend that you would expect, being correlated with the avg. L2 norm, and so all the rescaling types mostly follow the inverse of the average L2 by layer curve from before. For both L1 and MSE the linear approach seems quite bad, although both log and sqrt, particularly log, actually look better to me, in that they don’t increase the averages too much, and seem like they could have the desired effect of not overweighing the later layers with higher activations.

Shown below is the final FVU vs L0 of these runs, which has a few notable things.

img

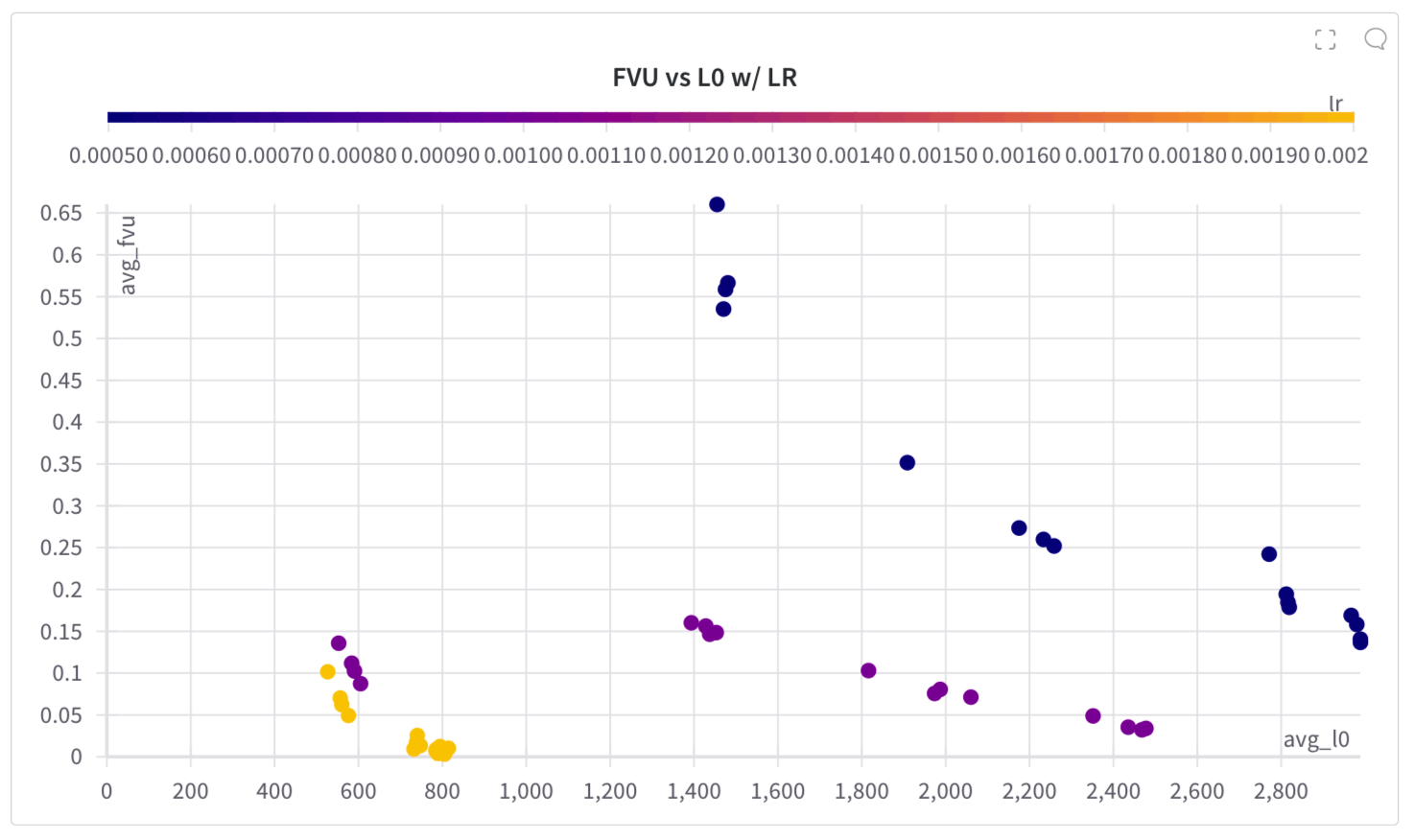
For one, the front improves with an increase in the already high learning rate, which is not what I would have expected, but may be a result of the relatively small amount of training data. Second, and this is only directly viewable on the interactive version linked, the runs which differ only by the rescaling type are all in clusters together, and in most cases become more sparse and lower in FVU going from no rescaling -> log -> sqrt -> linear. I’m unsure how useful this is, as the effect is small and has a worse curve than you would get from varying the L1 regularization factor. I do find it interesting though, as L0 is following a different trend from L1, so scaling the input activations can actually improve sparsity.

From all of this, I train another autoencoder on multiple layers using log activation rescaling and more activations (About 250 million). The full data can be found here5.

This autoencoder has some issues, namely that there are many features which activate with extremely high frequency, and a large number of dead neurons, issues that could be improved with some more hyperparameter tuning and adding neuron resampling. These shouldn’t matter for this proof of concept though, as I primarily want to see whether I can find any interpretable features which can occur across layers.

Shown below is the feature density of the final model, as log10(freq). Note that the discontinuity that occurs below ~10^-7 is a result of the length of the sliding window used to count occurrences, and that 10^-10 is the default value given to features which have not occurred in the window, and are almost certainly dead.

img

Results

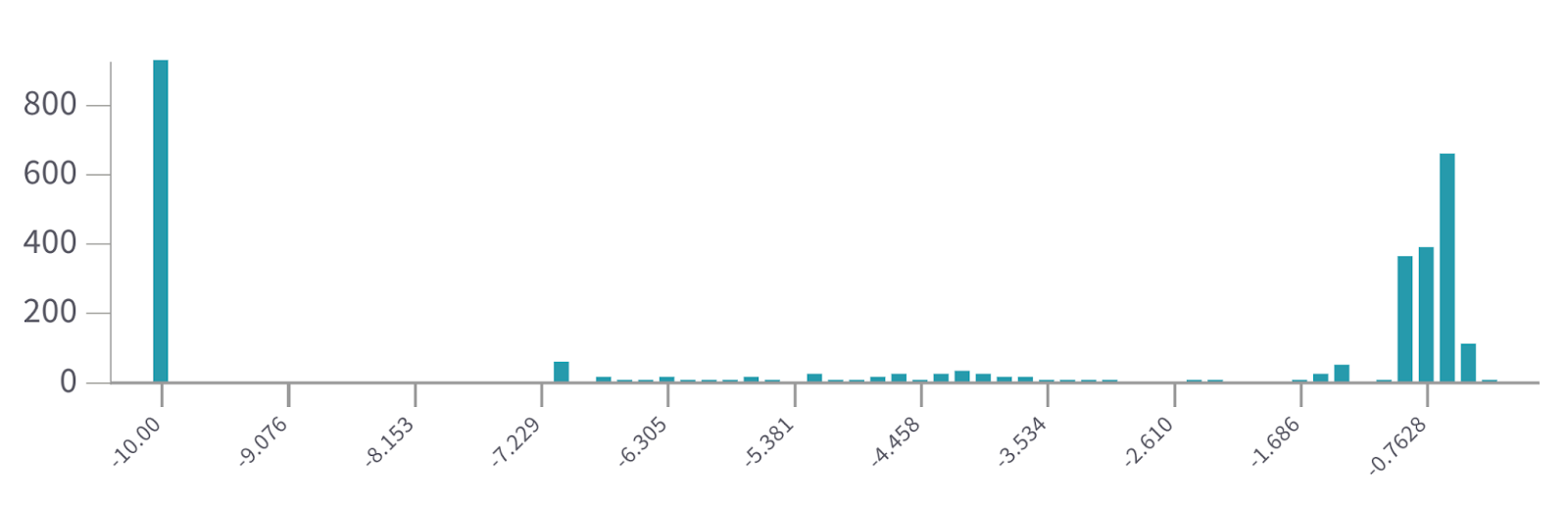
I primarily searched in the center of this distribution, around features with a frequency of ~1/10000, and found a few interesting features, examples of which are listed at the end. There are a few patterns I noticed in these:

  1. A feature can often be consistent within layers, even if it isn’t consistent between them. See Feature #1136, which activates on the “Sad” from “Sadie” and “wished” in layer 0, newlines in layer 2, and the space at the end of a line in layer 11.
  2. Features can activate on the same concept on different layers. Feature #23737 activates on newlines in the second and third layers. Perhaps more interestingly, Feature #5088 activates on the word “the”, but only in the first and last layers, which seems very odd. My intuitions were that the latent space of the residual stream was changing in such a way that made features only consistent in adjacent layers, perhaps there’s something special going on with the first and last layers representations.
  3. The final layer seems to have interpretable features more frequently, I don’t know if this is related to the problem of the growing residual stream norm mentioned earlier, or something else. There also seem to be a lot of features that fire specifically on names in the final layer - see this set of features9 which was randomly sampled* and has 8/20 which activate on names. This may be a result of using TinyStories, which has lots of names, particularly at the beginning of the stories, which my sampling favored.

*From a set of features that was filtered to have a certain activation frequency and distribution across layers, so maybe something else is going on.

A couple of ideas come to mind for further training/research:

  1. The autoencoder’s hidden size should be bigger, perhaps substantially so. I used 4 times the input dimension, partially a conceit to needing to run lots of tests fast, and I think this was far too small.
  2. A more diverse dataset would likely aid with feature analysis, as it is sometimes unclear whether a feature’s activations on different layers actually correlate as the range of themes/concepts in TinyStories is quite limited.
  3. Training on a subset of layers, either continuous or in some other arrangement like first/last, may lead to cleaner results and could also be faster to iterate upon

Notes on features:

  1. https://www.alignmentforum.org/posts/8mizBCm3dyc432nK8/residual-stream-norms-grow-exponentially-over-the-forward#Theories_for_the_source_of_the_growth ↩︎

  2. https://wandb.ai/collingray/multilayer_sae/groups/layer_lreg_sweep/workspace?nw=nwusercollingray ↩︎

  3. https://api.wandb.ai/links/collingray/2z27z7ue ↩︎

  4. https://wandb.ai/collingray/multilayer_sae/groups/renorm_lreg_sweep/workspace?nw=8kaxrdcaemb ↩︎

  5. https://wandb.ai/collingray/multilayer_sae/runs/hsnjbh9l ↩︎

  6. https://docs.google.com/document/d/1MnFc4C6CsyzZNmc3b-aduWUHLGR159qIsF4PQYkBHKA/edit#heading=h.kdnzcpnii76m ↩︎

  7. https://docs.google.com/document/d/1MnFc4C6CsyzZNmc3b-aduWUHLGR159qIsF4PQYkBHKA/edit#heading=h.fcpseoazvals ↩︎

  8. https://docs.google.com/document/d/1MnFc4C6CsyzZNmc3b-aduWUHLGR159qIsF4PQYkBHKA/edit#heading=h.dowak58z5lzf ↩︎

  9. https://docs.google.com/document/d/1MnFc4C6CsyzZNmc3b-aduWUHLGR159qIsF4PQYkBHKA/edit#heading=h.tz99gbnpcfsg ↩︎